Bijekcija

Pogreška pri izradbi sličice:

Bijektivna funkcija.

U matematici, za funkciju iz skupa X u skup Y kažemo da je bijektivna ako za svaki y u Y postoji točno jedan x u X takav da f(x) = y.

Drugim riječima, f je bijektivna je 1-1 korespondencija između tih skupova, tj. i 1-1 (injekcija) i na (surjekcija)

Na primjer, funkcija sljedbenika sljed, definirana na skupu cijelih brojeva $\mathbb {Z}$ u $\mathbb {Z}$, tako da svakom cijelom broju x pridjeljuje cijeli broj sljed(x) = x + 1. Za drugi primjer, neka se promotri funkcija sumraz koja svakom paru (x,y) realnih brojeva pridjeljuje par sumraz(x,y) = (x + y, x − y).

Bijektivna se funkcija još zove bijekcija ili obostrano jednoznačno preslikavanje ili permutacija. Potonji se termin češće koristi kad je X = Y. Valja uočiti da 1-1 funkcija nekim autorima znači 1-1 korespondencija (tj. bijekcija), a drugim autorima injekcija. Skup svih bijekcija iz Y u Y se označava kao X${}\leftrightarrow {}$Y.

Bijektivne funkcije imaju fundamentalnu ulogu u mnogim područjima matematike, poput definicije izomorfizma (i srodnih koncepata poput homeomorfizma i difeomorfizma), permutacijske grupe, projektivne ravnine, i mnogim drugim.

Kompozicija i inverzija

Funkcija f je bijektivna ako i samo ako je njezina inverzna relacija f ⁻¹ funkcija. U tom je slučaju f ⁻¹ također i bijekcija.

Kompozicija g o f dvaju bijekcija f$\;:\;$ X${}\leftrightarrow {}$Y i g$\;:\;$ Y${}\leftrightarrow {}$Z je bijekcija. Inverz od g o f je (g o f)⁻¹ = (f ⁻¹) o (g⁻¹).

Bijekcija komponirana od injekcije i surjekcije.

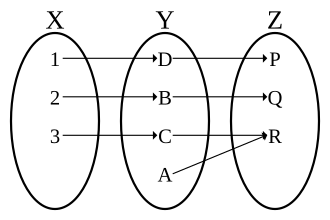
S druge strane, ako je kompozicija g o f dvaju funkcija bijektivna, možemo samo reći da je f injektivna i g surjektivna.

Relacija f iz X u Y je bijektivna funkcija ako i samo ako postoji druga relacija g iz Y u X takva da je g o f identiteta na X, i f o g je identiteta na Y. Slijedi da skupovi imaju isti kardinalni broj

Vidjeti također

• injekcija
• izomorfizam
• permutacija
• simetrična grupa
• surjekcija

Nedovršeni članak Bijekcija koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.